Perceived Brightness Index

[JCD]

Knowing the OTF lumens of a flashlight is good data to have. However, when comparing lights, lumens ratings are of limited value. This is because we perceive brightness in a generally logarithmic manner. Doubling the OTF lumens of a flashlight does not double the perceived brightness. I was wondering if anyone else might consider an index value for flashlights based on their relative perceived brightness to be useful.

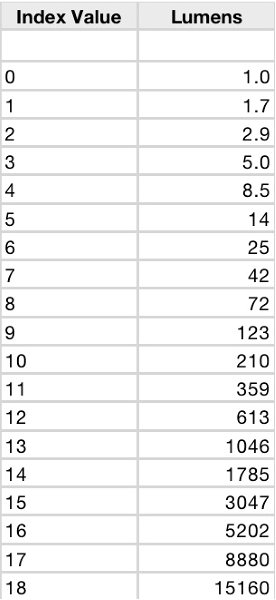
I put together the following chart based on logarithms of base 1+√(2)/2. (I obtained that base from this post.) Assuming the base number to be correct, then an increase or decrease of less than 1 in the index value would not yield a noticeable difference in brightness (to the naked eye). For example, a 170 lumen flashlight and a 210 lumen flashlight will appear to be approximately the same brightness. However, a 10 lumen flashlight would be noticeably brighter than a 5 lumen flashlight.

Or, put another way, lights with similar index values (a difference of less than one) are approximately equal in perceived brightness, so other factors should be considered more important when choosing between/among them for purchase or use.

I'm interested in feedback, including information regarding the best base number to use for a logarithmic scale.

Note that the following table is a starting point, and not a finished product. It may not be accurate in its present form and might require modification. The goal of starting this thread is to develop a scale that is reasonably accurate in order to compare the perceived brightness of different lights based on their OTF lumens.

To obtain the index value I for a flashlight with x OTF lumens:

I = ln(x) / ln(1+√(2)/2)

 

[Ragiska]

you're over two thousand years late

http://en.wikipedia.org/wiki/Stevens'_power_law

http://www.cis.rit.edu/people/faculty/montag/vandplite/pages/chap_6/ch6p10.html

http://en.wikipedia.org/wiki/Weber–Fechner_law

http://www.richardbrice.net/webers_law.htm

 

[Burgess]

Interesting thread. :twothumbs

I want to add one non-scientific item . . . .


My one flashlight (Low-Medium-High) produces (OTF):

roughly 60 Lumens on Medium
and
roughly 160 Lumens on High

In MY real life use, (outdoors, very rural setting),
there is such little noticeable difference between the two levels,
that i virtually never even Bother with High level.

Medium is almost as bright (to me, anyway)

and lasts LOTS longer !


This fact really surprised me, folks !

If i hadn't tried it for myself, i wouldn't have believed it.


_

 

[JCD]

you're over two thousand years late

http://en.wikipedia.org/wiki/Stevens'_power_law

http://www.cis.rit.edu/people/faculty/montag/vandplite/pages/chap_6/ch6p10.html

http://en.wikipedia.org/wiki/Weber–Fechner_law

http://www.richardbrice.net/webers_law.htm

Yes, I noted in my post that we know that our perception of brightness is logarithmic. I'm in no way claiming to have discovered anything. I was merely trying to apply that logarithmic quality in a manner useful to those who wish to be able to predict the perceived brightness between two lights based on their OTF lumens.

Astronomers use a similar system utilizing logarithm of base 10^(2/5), a system that has evolved since Hipparchus first ranked stars in six classes of magnitude. The Richter scale is a log base ten scale for measuring earthquake magnitude. The idea of the scale is nothing new, but as far as I was able to find, has not yet been applied to flashlights.

 

[JaguarDave-in-Oz]

Or, put another way, lights with similar index values (a difference of less than one) are approximately equal in perceived brightness, so other factors should be considered more important when choosing between/among them for purchase or use.

I'm interested in feedback, including information regarding the best base number to use for a logarithmic scale.

I look at the values in index values 9 and 10 and wonder are the values too far apart at that level.

I have no method of testing the actual lumens produced in my own torches but using factory specs to judge values when comparing my quark R5 on max with AA at a supposed 109 lumens with the same head on max with a CR123 at supposedly 206 lumens I perceive an absolutely massive difference, more than I'd call a "step" (a step would be a very subjective measure though, I admit).

Ok, yes, my torch has a 97 lumen "step" between those two batteries but that's not really that far apart from your chart's 87 lumen step and for me at that brightness range my eyes seem to regard a torch at the bottom of your range to be well dimmer than a torch towards the top and thus not really "approximately equal".

I don't know if that's because my eyes are attuned to seeing the difference between my many torches or because I when I use my torches at night it's usually in very very dark open spaces without much ambient light (unless it's full moon). In daylight I find it much harder to discern the smaller differences in brightness.

I've no idea if any of this rambling of mine assists you to form a view on the value of your chart's values/base or not. I do agree that such a chart has vlaue though. It would be nice to have something to help dampen the focus on lights being thought of as ten or twenty lumens "better".

 

[Ragiska]

Yes, I noted in my post that we know that our perception of brightness is logarithmic. I'm in no way claiming to have discovered anything. I was merely trying to apply that logarithmic quality in a manner useful to those who wish to be able to predict the perceived brightness between two lights based on their OTF lumens.

Astronomers use a similar system utilizing logarithm of base 10^(2/5), a system that has evolved since Hipparchus first ranked stars in six classes of magnitude. The Richter scale is a log base ten scale for measuring earthquake magnitude. The idea of the scale is nothing new, but as far as I was able to find, has not yet been applied to flashlights.

yes, they have already been applied to flashlights over 100 years ago. each light emission pattern has a unique multiplier.

 

[JCD]

Thanks for the feedback.

I look at the values in index values 9 and 10 and wonder are the values too far apart at that level.

I have no method of testing the actual lumens produced in my own torches but using factory specs to judge values when comparing my quark R5 on max with AA at a supposed 109 lumens with the same head on max with a CR123 at supposedly 206 lumens I perceive an absolutely massive difference, more than I'd call a "step" (a step would be a very subjective measure though, I admit).

Using the current base (approximately 1.71) 109 lumens would correspond to an index value of 8.77. 206 lumens would correspond to an index value of 9.96. The difference between the to is 1.19. So, we would expect to see a difference, but not an "absolutely massive difference."

I see a few possibilities for the large perceived brightness difference you're seeing around the 9 - 10 index values.

First, the base for the logarithm could be incorrect. If that's the case, then I would expect that error would become more apparent as the index values increased.

A related possibility is that people perceive brightness differently depending on the wavelength of the light. Perhaps the base of the logarithm should not be a constant, but rather a function of the color temperature or other quality of the light.

Another related possibility is that our sensitivity to brightness varies as the brightness varies.

It's possible (and probable) that different individuals likely have slightly different sensitivities to brightness. Yours might be more sensitive than most, due to genetics, or environmental factors (e.g., your flashlight hobby could have allowed you to develop a keener sensitivity to brightness).

Another possibility is that the advertised lumens of your Quark are incorrect relative to the particular light you received. This itself could be due to an over/understatement of brightness by the manufacturer, or just variation in the emitters they used. This possibility would be the easiest to accurately test, since the tests would be completely objective.

I have a Fenix PD30 with a brightness index step of 1.19 from high to turbo. Tonight, I'll put some primaries in it, and see how large that difference appears to me (not very scientific, since I already know the index step and can't immediately verify the accuracy of the lumens rating, but it's slightly better than nothing). From medium to high there is a step of 0.96, so that one should barely be noticeable if the base is correct.

Did you compare the brightness levels of your Quark on a white wall, or in a real world situation (e.g., outdoors)?

 

[JCD]

yes, they have already been applied to flashlights over 100 years ago. each light emission pattern has a unique multiplier.

Perhaps you would be kind enough to link to a source (or provide the necessary info to locate the source in a library) showing where such an index has been in existence for flashlights for over a century. That index would be extremely useful for CPF members, so it would be great to have access to it.

 

[Ragiska]

Perhaps you would be kind enough to link to a source (or provide the necessary info to locate the source in a library) showing where such an index has been in existence for flashlights for over a century. That index would be extremely useful for CPF members, so it would be great to have access to it.

already did, Stevens' Power Law (linked above) has at least five brightness related stimulus conditions.

 

[RedForest UK]

Well personally stevens power law wasnt even on my radar until this thread was set up so without taking anything away from the original law all credit to the OP for bringing this index to many more peoples attention.

I'm sure that if people are sufficently interested by it then they will look into the subject further and find out other perhaps prior laws and indexes as well. Thanks for providing some links to facilitate further reading, but please don't take away from the OP's efforts to bring this to more peoples attention simply for the sake of it. IMO this simple table is a much easier way of understanding the increased difference in lumens needed to create the same apparent difference in 'actual' percieved brightness than the slightly obscure references provided by stevens law.

 

[chenko]

I couldn't agree more with RedForest UK. Thanks JCD!

 

[JCD]

already did, Stevens' Power Law (linked above) has at least five brightness related stimulus conditions.

The links you previously posted do not provide the necessary information for a suitable perceived brightness scale.

If we use Stevens' law, we are interested in the sensation magnitude S. Substituting 1/2 for the measured exponent for a point source (per Stevens' values), the equation becomes , S = k·√(I). Clearly this is not a logarithmic equation (although that doesn't mean it's wrong), so if it is correct, my initial assumption that we perceive brightness logarithmically is incorrect.

Since it is not a logarithmic equation, one lumen can't provide a sensation magnitude of 0 as a logarithmic scale would provide. That's fine. We can arbitrarily give a 1 lumen point source a sensation magnitude of 1. This arbitrarily gives us k=1·√(lumens)/lumens.

So, for:

S=1, Intensity = 1 lumen
S=2, Intensity = 4 lumens
S=3, Intensity = 9 lumens
S=4, Intensity = 16 lumens
S=5, Intensity = 25 lumens
S=6, Intensity = 36 lumens
S=7, Intensity = 49 lumen
S=8, Intensity = 64 lumen
S=9, Intensity = 81 lumen
S=10, Intensity = 100 lumen

etc.

The first problem that immediately jumps out is that arbitrarily assigning a one lumen torch a Sensation magnitude of 1 eliminates any useful meaning of an increase of 1 to the sensation magnitude value. So, before Stevens' law can potentially serve our purpose, we have to find a suitable non-arbitrary value of k when using lumens as our unit for stimuli intensity.

Even without knowing the correct value for k, we can check to see if the predictions seem reasonable. Each equal step in S should offer an approximately equal incremental change in perceived brightness. I would hypothesize that a four lumen torch is much brighter relative to a 1 lumen torch than a 100 lumen torch is, relative to an 81 lumen torch.

Edit to add:
I just noticed that I used the Stevens measured exponent for looking into the light, not looking at the area illuminated. The closest Stevens offers for comparing brightness of the area illuminated the measured exponent associated with "5º target in dark." That would change our formula such that S increases with the cube root of I instead of with the square root of I. So, the formula would predict that increasing from 1 lumen to 8 lumens should yield the same proportional increase in brightness as an increase from 729 lumens to 1000 lumens. I do not believe this to be a reasonable prediction. (End edit)

Of course, mine are not the only criticisms of Stevens' law.

The Weber-Fechner law tells us that perceived intensity is a logarithmic function of stimuli intensity, but it doesn't provide us with real world numbers so our function can fit the data related to the specific stimulus type we are looking for, so that we might make meaningful predictions. That is the very information we are trying to obtain in this thread. Without it, the W-F law isn't very useful for us.

 

[Niconical]

Ragiska, do you have anything to actually contribute, or do you just want to repeatedly point out that at some time in the past someone else has done similar calculations?

As to this principle having been applied to flashlights "100 years" ago, that was no doubt handy for early 20th century flashaholics, but it aint much us on the forum though, is it?

I don't normally comment on such things, but JCD took the time and effort to put an idea into an easy to use reference form for the forum to discuss, and the first reply is "you're 2000 years late".

My point is, if you have something to say, say it, if you just want to bring down, complain, pick, whatever the word is, we don't need that, especially in a thread where someone has taken the time to contribute.

Personally I think this is a great thing JCD has done, something to link to when members are wondering over the 220 lumen or the 240. This will help to put that all into perspective.

 

[JCD]

Well personally stevens power law wasnt even on my radar until this thread was set up so without taking anything away from the original law all credit to the OP for bringing this index to many more peoples attention.

I'm sure that if people are sufficently interested by it then they will look into the subject further and find out other perhaps prior laws and indexes as well. Thanks for providing some links to facilitate further reading, but please don't take away from the OP's efforts to bring this to more peoples attention simply for the sake of it. IMO this simple table is a much easier way of understanding the increased difference in lumens needed to create the same apparent difference in 'actual' percieved brightness than the slightly obscure references provided by stevens law.

Thank you (and others) for the kind words. I want to clarify that the table I provided is not necessarily accurate. It requires assumptions that we have not yet verified to be accurate. In particular, the base of the logarithmic function needs to be verified. (I can write the equation in a different way to simply make that unknown a constant (or function) of proportionality.)

At a minimum, accurate lumens ratings and a lot of A-B comparisons (brighter, the same, dimmer?) of many lights from many people. It might also be necessary to have accurate color temperature readings of each light.

So, at this point, the table in post 1 is a starting point only. I expect it to be modified before it is accurate. But, we have to start somewhere, and, collectively, CPF members have the resources to develop a useful index. I don't doubt that we can make it happen. My hope is that we will make it happen.

 

[Ragiska]

i recommend a paper titled "the visual discrimination of intensity and the weber-fechner law" by selig hecht.

 

[JCD]

i recommend a paper titled "the visual discrimination of intensity and the weber-fechner law" by selig hecht.

The table in the first post of this thread is based on the Weber-Fechner law, where ∆I/I = (√(2)/2)/1 = √(2)/2.

The Hecht paper seems to imply that the formula we are looking for will have the form P = f(I)·ln(I) + C instead of P = k·ln(I) + C.

 

[BigHonu]

I put together the following chart based on logarithms of base 1+√(2)/2. (I obtained that base from post 4 in this thread.) Assuming the base number to be correct, then an increase or decrease of less than 1 in the index value would not yield a noticeable difference in brightness (to the naked eye). For example, a 170 lumen flashlight and a 210 lumen flashlight will appear to be approximately the same brightness. However, a 10 lumen flashlight would be noticeably brighter than a 5 lumen flashlight.

Or, put another way, lights with similar index values (a difference of less than one) are approximately equal in perceived brightness, so other factors should be considered more important when choosing between/among them for purchase or use.

To obtain the index value I for a flashlight with x OTF lumens:

I = ln(x) / ln(1+√(2)/2)

JCD,

Great start to an overlooked topic. With the ever growing race to produce products that maximize output, I think a lot of people loose sight of the fact that bumping up the current to go from 350 lumens to 450 lumens may not be beneficial from a practical standpoint as most of us would find it difficult to 'see' the difference.

I am not qualified to comment on the math behind your scale, but it seems that you are trying to define the smallest step up in lumens (relative to the previous step) that would give a perceptual increase in brightness? How would I define a light on this scale that is about twice as bright as another light? Would the assumption be that in order to compare lights on this Index, they would have to be of a similar beam pattern? I know that non-flashaholics would say that an XX lumen pencil beam is brighter than an XX lumen flood.

Thanks for your time, and I applogize if the answers to my questions are self-evident in your table.

 

[JCD]

… it seems that you are trying to define the smallest step up in lumens (relative to the previous step) that would give a perceptual increase in brightness?

Yes, that is the goal.

How would I define a light on this scale that is about twice as bright as another light?

Do you mean twice as bright in terms of lumens produced by the light or in terms of perceived brightness? Doubling lumens would result in an increase of about 1.3 in the perceived brightness index number. I'm not sure how large an increase in the index would be caused by doubling perceived brightness.

Would the assumption be that in order to compare lights on this Index, they would have to be of a similar beam pattern?

Honestly, I'm not quite sure. Ideally, it will work across all beam types, like an integrating sphere. However, we don't live in an ideal world, and experimental data may reveal that, all else equal, one beam type is generally perceived to be brighter than a second beam type. That, too, would prove to be useful information.

I think the usefulness will come from being able to see that relative brightness between two lights shouldn't always be an important consideration. For example, if someone is considering Light A and Light B, if Light A produces 15% more lumens, but Light B has a nicer beam and warmer tint, their respective perceived brightness index values would show that the increased brightness of Light A isn't great enough to sacrifice the beam quality or tint of Light B.

Thanks for your time, and I applogize if the answers to my questions are self-evident in your table.

No apology is necessary. I don't believe the answers were self evident.

 

[BigHonu]

Do you mean twice as bright in terms of lumens produced by the light or in terms of perceived brightness? Doubling lumens would result in an increase of about 1.3 in the perceived brightness index number. I'm not sure how large an increase in the index would be caused by doubling perceived brightness.

Oops, sorry I wasn't clear. In terms of the Index. I suppose it would be advantageous at some point to be able to say that in general, moving up 'X' index spots would be about a doubling of perceived brightness.

Honestly, I'm not quite sure. Ideally, it will work across all beam types, like an integrating sphere. However, we don't live in an ideal world, and experimental data may reveal that, all else equal, one beam type is generally perceived to be brighter than a second beam type. That, too, would prove to be useful information.

I think the usefulness will come from being able to see that relative brightness between two lights shouldn't always be an important consideration. For example, if someone is considering Light A and Light B, if Light A produces 15% more lumens, but Light B has a nicer beam and warmer tint, their respective perceived brightness index values would show that the increased brightness of Light A isn't great enough to sacrifice the beam quality or tint of Light B.

I understand the goal, and think that beam profile considerations will bring an unecessary level of complexity to this index. However, through exeperience, I do know that a more focused beam will tend to be perceived as being brighter even if I qualify 'brighter' as being the total amount of light.

Again, thanks for putting this out there.

 

[TEEJ]

I just found this thread....sorry to drag it up from the grave...albeit It occurred to me that we can't actually see lumens, and the the perceived brightness of the flashlight is really due to what reflects back off of a target...lets call that the Lux on the target perhaps.

This means that a beam pattern with a large spill/corona will be perceived differently than a tight hot beam..because the same lumens will all be in a smaller area for a thrower, and a larger area for a flooder.

If I have 1,000 lumens, and I shine them in a beam that makes a solid 1 m2 circle of light on my target, I will see 1,000 lux.

If that same emitter is projecting a floody 10 m2 circle of light, I will only see 100 Lux....and it will look dimmer.

So, if we want to say a light has to have twice the lumens to be able to tell its brighter...we should also consider that it could in fact even have half the lumens and look brighter, etc.

I think for a floody light at least, I don't need it to produce twice the lux for me to be able to tell it is brighter....but for a thrower, especially at close range, the hot spot tends to stop my eyes down after a point of diminishing return, essentially, once its as bright as I can see, I won't know if it got brighter, only if the spot enlarged, etc....kind of my eye's light meter overloading/being off scale.

So, the dogma about "needing twice the lumens to tell a difference" when the context is comparing two different lights for example is misleading.